Recurrent Neural Network Model

Why not a standard model?

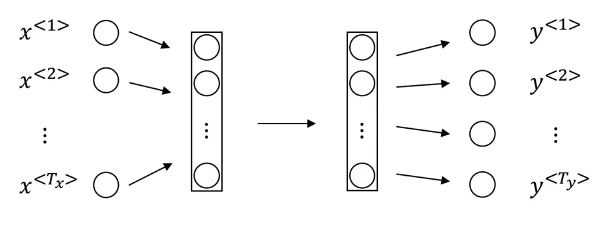
Problems:

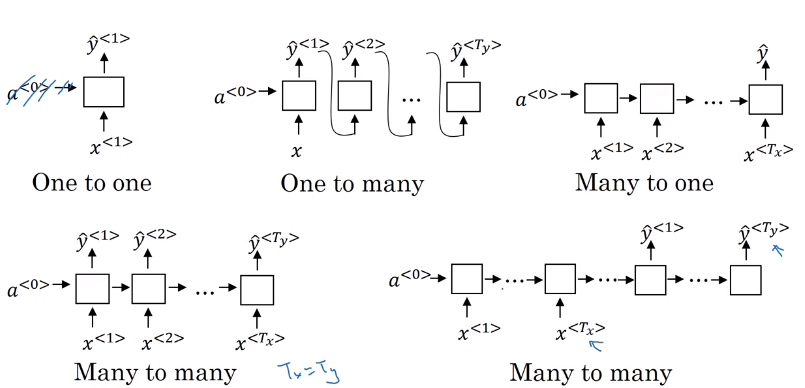
Inputs, outputs can be different lengths in different examples.

Doesnt share fearues learned across different positions of text

RNN

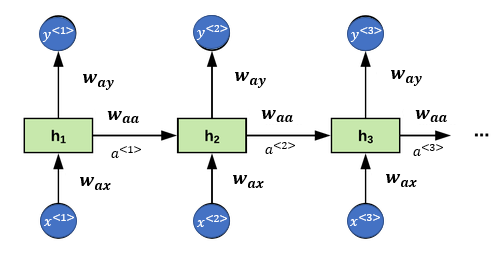
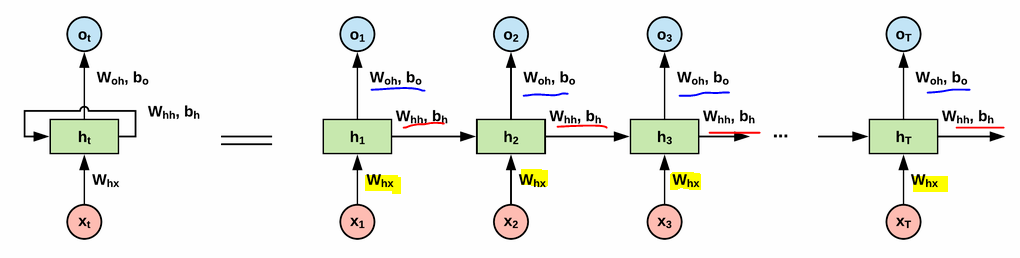parameters are shared

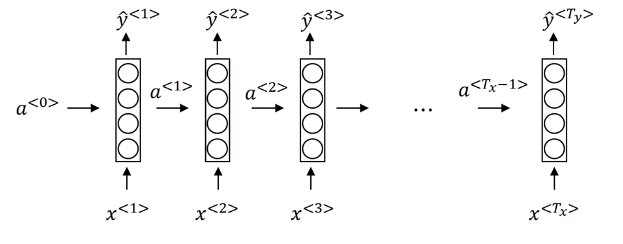
One weakness of this RNN is that it only uses the information that is earlier in the sequence to make a prediction.

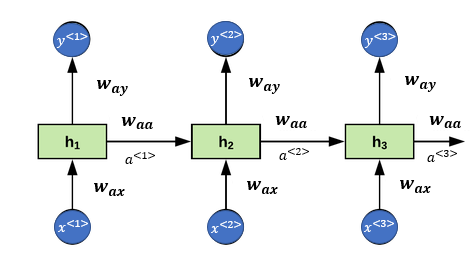
• Start with $a^{<0>}=\vec{0}$

• $a^{<1>}=g(W_{aa}a^{<0>}+W_{ax}x^{<1>}+b_a)$

• $\hat{y}^{<1>}=g(W_{ya}a^{<1>}++b_y)$

$a\rightarrow W_{ax}X^{<1>}$
The second index $x$ means that this $W_{ax}$ is going to be multiplied by some $X$-like quantity, and The first index $a$ means that this is used to compute some $a$-like quantity

$W_{ya}$ is multiplied by some $a$ like quantity to compute a $y$ type quantity.

In RNN, tanh is very common choice. ReLu is sometimes used.

In generalized way

• $a^{<t>}=g(W_{aa}a^{<t-1>}+W_{ax}x^{<t>}+b_a)$

• $\hat{y}^{<1>}=g(W_{ya}a^{<t>}+b_y)$ g will depends on what y as usual

This can be rewritten as:

• $a^{<t>}=g(W_{a}[a^{<t-1>},x^{<t>}]+b_a)$
• $W_a=[W_{aa} W_{ax}]$

If $a$ was a 100 dimensional, and $x$ was 10,000 dimensional, then $W_{aa}$ would have been a 100 by 100 dimensional matrix, and $W_{ax}$ would have been a 100 by 10,000 dimensional matrix.

$[a^{<t-1>},x^{<t>}]$=$\begin{bmatrix} a^{<t-1>}\\ x^{<t>} \end{bmatrix}$

Backpropagation through time

Forward and backword Propagation

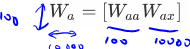
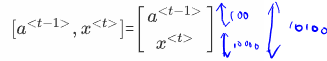
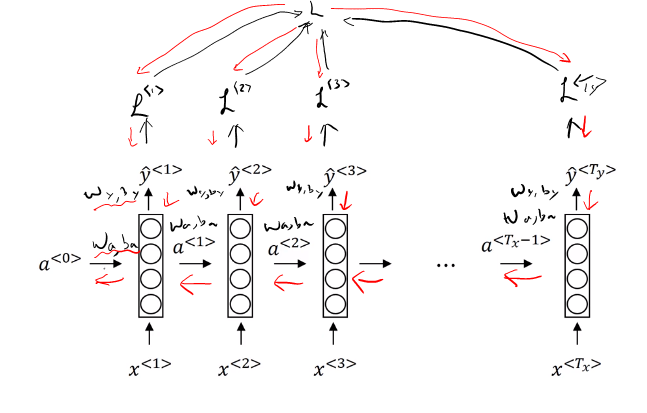
Backpropagation through time

Loss Function $\mathcal{L}^{<t>}(\hat{y}^{<t>},y^{<t>})=-y^{<t>}\log \hat{y}^{<t>}-(1-y^{<t>})\log (1-\hat{y}^{<t>})$

Overall loss of sequence

$\mathcal{L}(\hat{y},y)=\sum_{t=1}^{T_x}\mathcal{L}^{<t>}(\hat{y}^{<t>},y^{<t>})$

Different types of RNN

Andrej Karpathy http://karpathy.github.io/2015/05/21/rnn-effectiveness/

Many to Many Architecture

Many to One Architecture

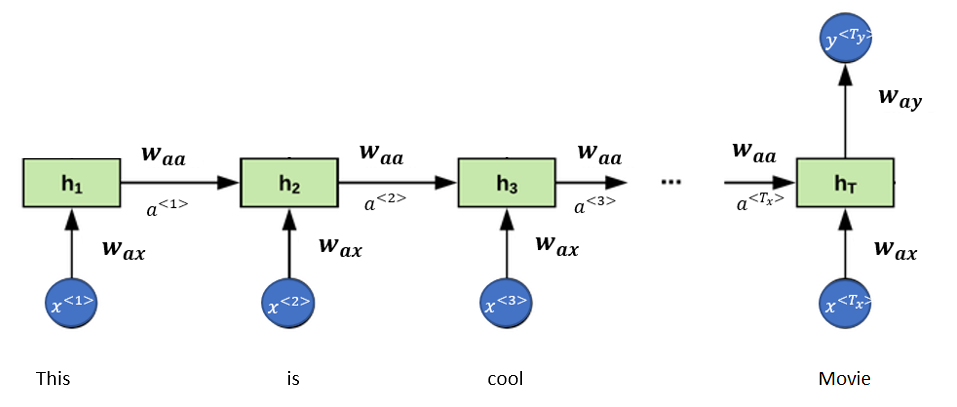
Use case: Sentence Classification

One to Many Architecture

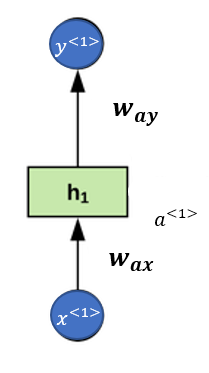
Use case: Music generalizations

Other many to many architecture

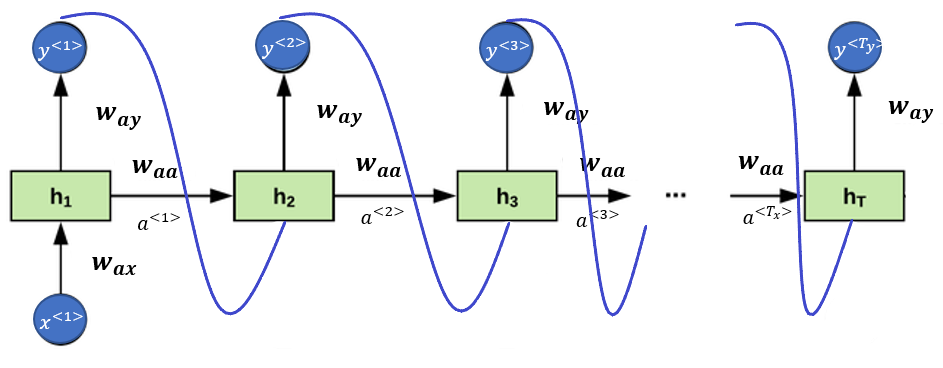
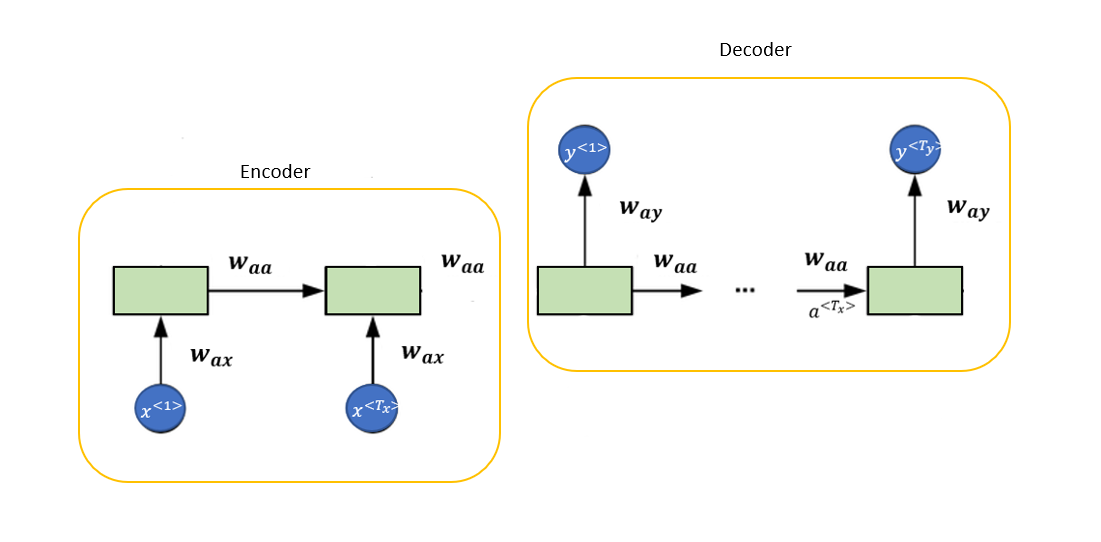
Translation

RNN cell forward

def rnn_cell_forward(xt, a_prev, parameters):
    """
    A single forward step of the RNN-cell
 
    Arguments:
    xt -- Input data at timestep "t", numpy array of shape (n_x, m).
    a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m)
    parameters -- python dictionary containing:
                        Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
                        Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
                        Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
                        ba --  Bias, numpy array of shape (n_a, 1)
                        by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
    Returns:
    a_next -- next hidden state, of shape (n_a, m)
    yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m)
    cache -- tuple of values needed for the backward pass, contains (a_next, a_prev, xt, parameters)
    """
 
    Wax = parameters["Wax"]
    Waa = parameters["Waa"]
    Wya = parameters["Wya"]
    ba = parameters["ba"]
    by = parameters["by"]
 
 
    a_next =np.tanh(np.dot(Wax,xt)+np.dot(Waa,a_prev)+ ba)
    yt_pred = softmax(np.dot(Wya,a_next) + by)
 
    cache = (a_next, a_prev, xt, parameters)
 
    return a_next, yt_pred, cache
 

RNN Forward pass

def rnn_forward(x, a0, parameters):
    """
    Implement the forward propagation of the recurrent neural network described in Figure (3).
 
    Arguments:
    x -- Input data for every time-step, of shape (n_x, m, T_x).
    a0 -- Initial hidden state, of shape (n_a, m)
    parameters -- python dictionary containing:
                        Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
                        Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
                        Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
                        ba --  Bias numpy array of shape (n_a, 1)
                        by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
 
    Returns:
    a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x)
    y_pred -- Predictions for every time-step, numpy array of shape (n_y, m, T_x)
    caches -- tuple of values needed for the backward pass, contains (list of caches, x)
    """
 
    # Initialize "caches" 
    caches = []
 
    # Retrieve dimensions from shapes of x and parameters["Wya"]
    n_x, m, T_x = x.shape
    n_y, n_a = parameters["Wya"].shape
 
    # initialize
    a = np.zeros([n_a,m,T_x])
    y_pred = np.zeros([n_y,m,T_x])
    a_next =a0
 
    # loop over all time-steps
    for t in range(T_x):
        # Update next hidden state, compute the prediction, get the cache
        a_next, yt_pred, cache =  rnn_cell_forward(x[:,:,t], a_next, parameters)
        # Save the value of the new "next" hidden state in a
        a[:,:,t] = a_next
        y_pred[:,:,t] = yt_pred
        caches.append(cache)
 
    caches = (caches, x)
 
    return a, y_pred, caches