deeplearning

Softmax Regression

There’s a generalization of logistic regression called Softmax regression. The less you make predictions where you’re trying to recognize one of C or one of multiple classes, rather than just recognize two classes.

Here is an example. Let’s say that we want to recognize cats, dogs, baby chicks, and other.

When we build a neural network, we have 4 output units. So, $n^{[L]}=4=C$

Output unit is computing $P(‘other’

x), P(‘cat’

x), P(‘dog’

x), P(‘chick’

x),$ and $\hat{y}$ is (4,1) shape. The standard model for getting your network to do this uses what’s called a Softmax layer, and the output layer in order to generate these outputs.

The final layer of the neural network is computing the following:

$z^{[L]}=W^{[L]}a{[L-1]}+b^{[L]}$

Activation function

• Temporaly variable: $t=e^{(z^{[L]})}$, (4,1)

• Then the output a{[L]}, is going to be basically the vector $t$ but normalized to sum to 1.
• $a^{[L]}=\frac{e^{(z^{[L]})}}{\sum_{j=1}^{4}t_i}$, (4,1) and
• $a^{[L]}i=\frac{t_i}{\sum{j=1}^{4}t_i}$

Example

Let $z^{[l]}=\begin{bmatrix} 5
2
-1
3 \end{bmatrix}$

Use element-wise exponentiation to compute $t$

$t=\begin{bmatrix} e^5
e^2
e^{-1}
e^3 \end{bmatrix}=\begin{bmatrix} 148.4
7.4
0.4
20.1 \end{bmatrix}$ then sum up t

$\sum^4_{j=1}t_j=148.4+7.4+0.4+20.1=176.3$

and $a^{[L]}=\frac{t}{176.3}$

Therefore, the first unit of the output layer will output $\frac{e^5}{176.3}=0.842$

We can compute for all 4 output units as follow:

$\frac{e^5}{176.3}=0.842$

$\frac{e^2}{176.3}=0.042$

$\frac{e^-1}{176.3}=0.002$

$\frac{e^3}{176.3}=0.114$

then $a^{[l]}=g^{[l]}(z^{[L]})=\hat{y}$ will contain above 4 numbers.

Unlike other activation function such as sigmoid function which takes $\mathbb{R}$ and returns $\mathbb{R}$, sigmoid function will return a vector.

Examples of Softmax

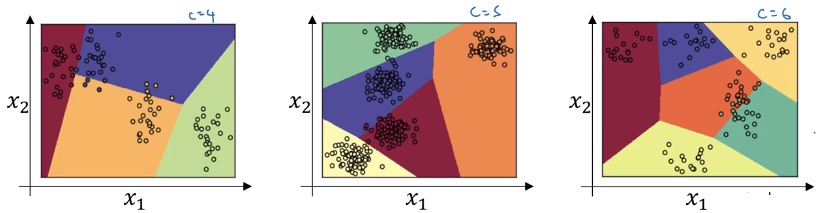
C=3

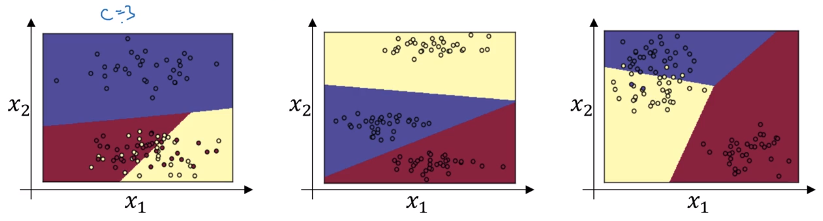
Note that the decision boundary are linear.

C=4, 5, 6